量子コンピータシュミレーションで可能性の検証

1.まえがき

　量子コンピュータは現在多くの国や企業で開発競争となっています。
　しかし、現在開発実機のあるものは、量子アナログ式(量子イジングマシン方式）で，理想的な量子デジタル式（量子ゲート方式）はまだ実現に至っていない。
　量子アナログ式(量子イジングマシン方式）は特殊な用途向きで、量子デジタル式（量子ゲート方式）は汎用性のある古典コンピータよりの置き換えが可能なものであ。。
　よって、Microsoftが2017/12に提供を開始した量子コンピータ開発環境(Quantum Development Kit)での検証から開始し、
　ハードが出来るまでにソフト側も並行して進行させる事を目的とします。

2.Microsoft提供の量子コンピータ開発環境(Quantum Development Kit)について

　　　2017/12/11提供開始した量子コンピータ開発環境で言語はQ#です。
　　　動作はVS.Netの環境下で動作し、C#・F#・VB.Net等より利用可能。
　　　量子コンピータシュミレーターはCPUのAdvance Vector Extensions (AVX) を利用し、その為AVX が有効な CPU(Q1 2011(Sandy Bridge) 以降) を必要となります。
　　　また、動作ＯＳは64Bitのみとなります。
　　　VS.Netのバージョンは2017以降が必要です。

3.動作(サンプルで検証)例

　　　C#よりQ#経由で量子コンピータシュミレーターを操作しています。
　　　-1.量子ビットと発生確率について(Measurement)
　　　　　Q#のFunction　MeasurementOneQubit・MeasurementTwoQubits・MeasurementBellBasis

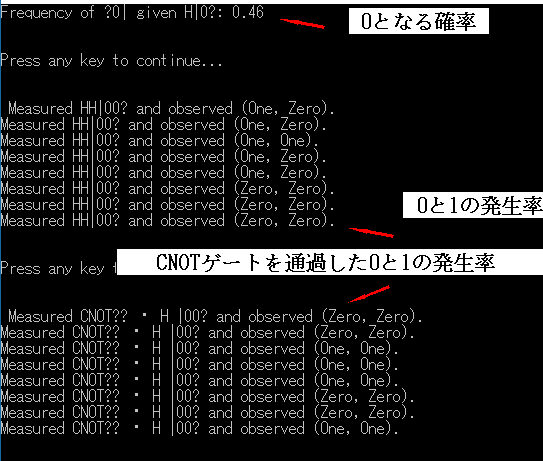
　　　　　a.0が出る確率　　　大体50%(0.5)
　　　　　b.0と1が出る割合　 00・01・10・11等ばらつきがある
　　　　　c.CNOTゲート後の割合　00と11に纏まっている

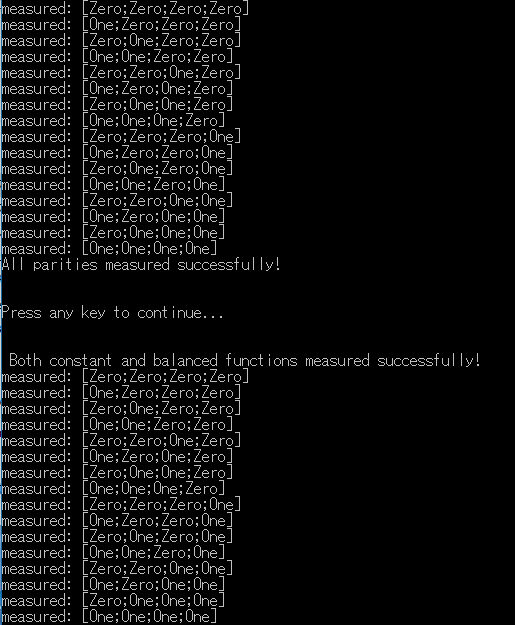
　　　-2.量子アルゴリズム(SimpleAlgorithms)
　　　　　a.Bernstein-Vaziraniアルゴリズム　パリティ演算を実施するBernstein-Viziraniのフーリエサンプリングアルゴリズム(4量子ビットの例)
　　　　　Q#のFunction　BernsteinVaziraniTestCase
　　　　　b.Deutsch-Joszaアルゴリズム　　　均一か等分かを判定するアルゴリズム
　　　　　Q#のFunction　DeutschJozsaTestCase
　　　　　c.Roettelerアルゴリズム　　　　　 Bent関数の隠れシフト問題を解くための相関アルゴリズム
　　　　　Q#のFunction　HiddenShiftBentCorrelationTestCase

　　　-3.量子テレポーテーション(TeleportationSample)
　　　　　Q#のFunction　TeleportClassicalMessage

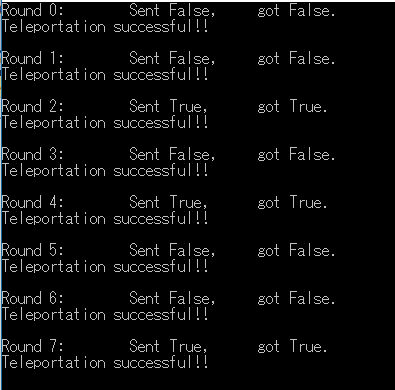　　　送りと受信が一致していると成功

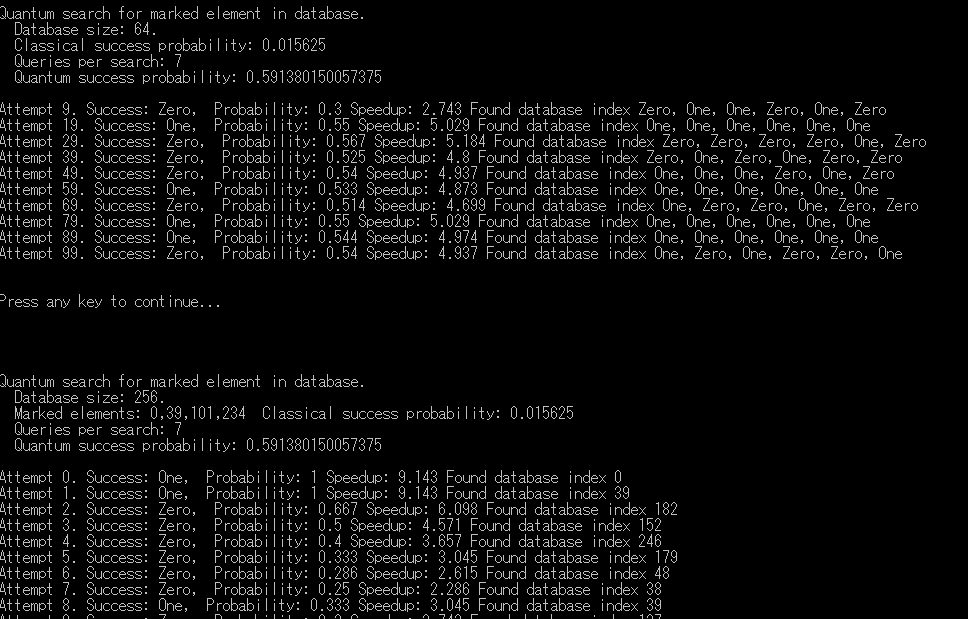
　　　-4.データベースサーチ(DatabaseSearchSample)
　　　　　Q#のFunction　ApplyQuantumSearch・ApplyGroverSearch
　　　　　Grover Search ランダムなデータベースの探索アルゴリズムである
　　　　　データベースサイズを8->64->256

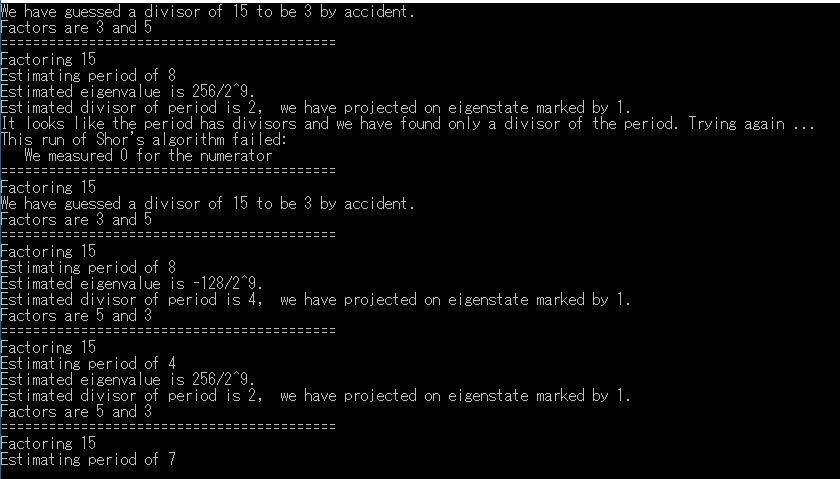
　　　-5.整数因子分解(IntegerFactorization)
　　　　　Q#のFunction　Shor
　　　　　15を整数因子分解(Robust Phase Estimationにて)を100回の例、正解は3と5
　　　　　途中で失敗もあり、量子コンピュータではこれらを選別する必要があり
　　　　　この機能により、今までの暗号解読を高速でできる可能性があります。

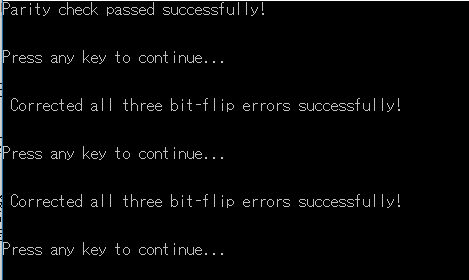
　　　-6.Parity Check、Correction Check、Correction Check with the Canon(BitFlipCode)
　　　　　Q#のFunction　CheckBitFlipCodeStateParity・CheckBitFlipCodeCorrectsBitFlipErrors・CheckCanonBitFlipCodeCorrectsBitFlipErrors
　　　　　α|0> + β|1>　-->　α |000> + β |111>の変換でチェック

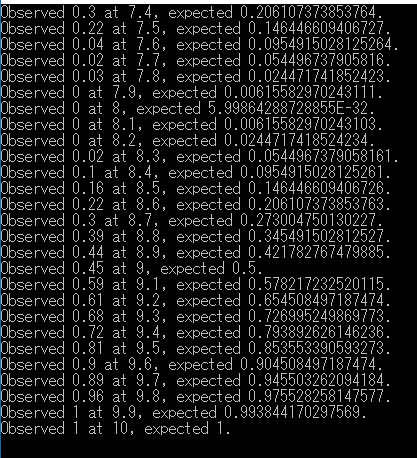
　　　-7.量子位相推定アルゴリズム (PhaseEstimationSample)
　　　　　Q#のFunction　PhaseEstimationIterationCheck
　　　　　Iterative phase estimation

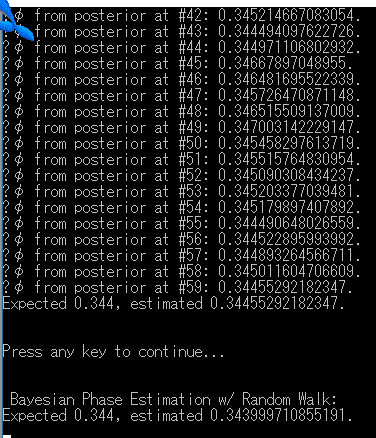
　　　　　Q#のFunction　BayesianPhaseEstimationSample・BayesianPhaseEstimationCanonSample
　　　　　Bayesian phase estimation

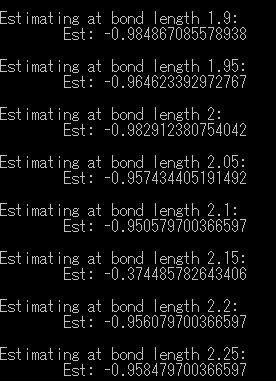
　　　-8.水素シュミレーション(H2SimulationSampleCmdLine)
　　　　　Q#のFunction　H2EstimateEnergyRPE
　　　　　２つの水素原子が結合している水素分子に対して、結合の長さ R とエネルギー固有値をシミュレーションします。
　　　　　結合の長さに対してエネルギー固有値を表示

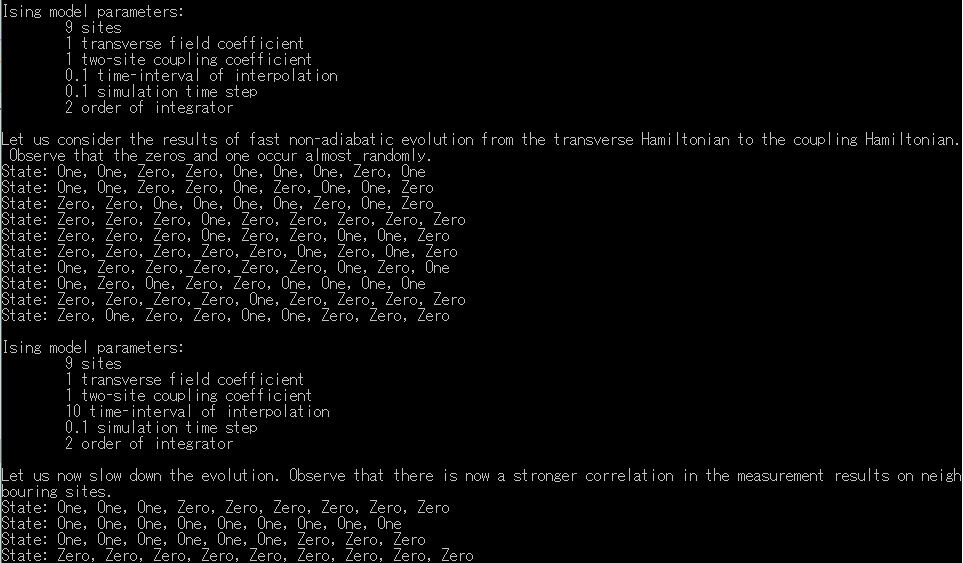
　　　-9.断熱イジング(AdiabaticIsingSample)
　　　　　Q#のFunction　Ising1DAdiabaticAndMeasureManual・Ising1DAdiabaticAndMeasureBuiltIn
　　　　　量子力学における断熱定理
　　　　　Ising Model（イジングモデル）とは、結晶を構成する原子の「スピン」の向きを計算する簡易的なモデルです。
　　　　　原子は温度が高いと激しく運動し、低いと鈍くなります、絶対零度（-273.15 ℃）になると完全に静止します。

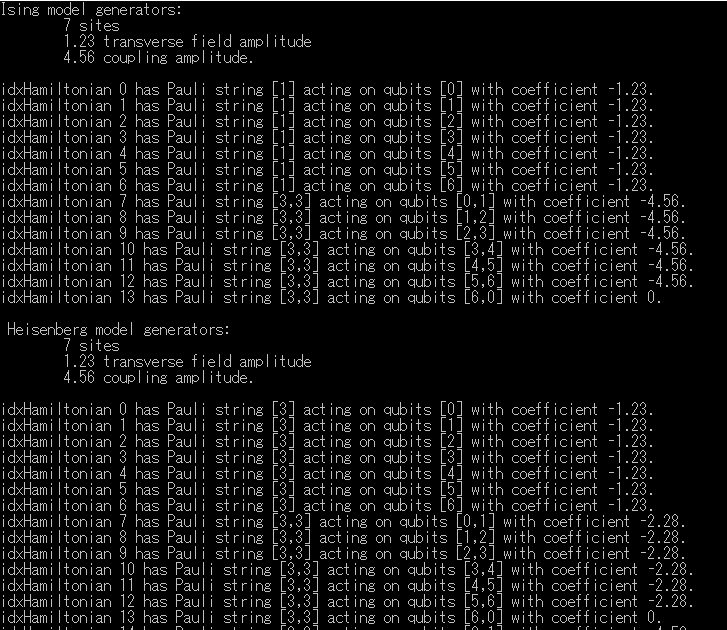
　　　-10.イジングモデルジェネレータ(IsingGeneratorsSample)
　　　　　Q#のFunction　Ising1DUnpackEvolutionGenerator
　　　　　Ising model generators(Ising1DUnpackEvolutionGenerator)
　　　　　Q#のFunction　HeisenbergXXZUnpackGeneratorSystem
　　　　　Heisenberg model generators(HeisenbergXXZUnpackGeneratorSystem)
　

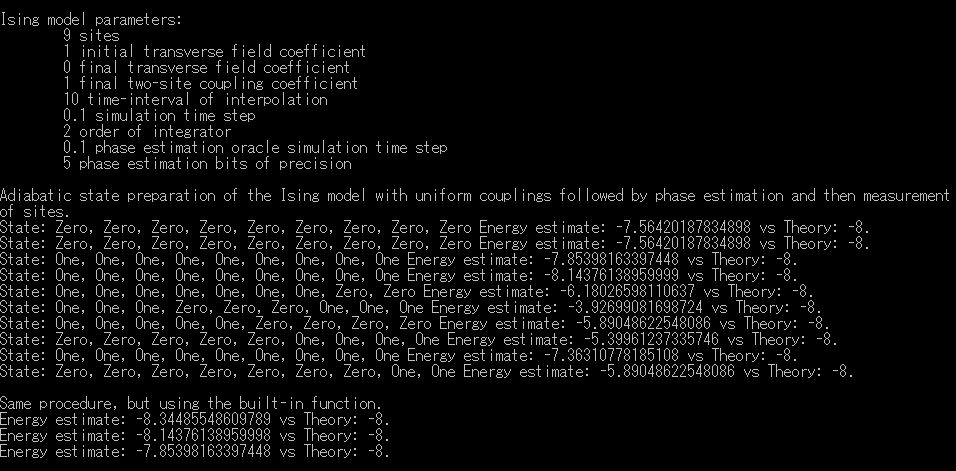
　　　-11.イジング位相を推定(IsingPhaseEstimationSample)
　　　　　エネルギー最小化問題
　　　　　Q#のFunction　IsingEstimateEnergy
　　　　　イジングエネルギーを推定(IsingEstimateEnergy)
　　　　　Q#のFunction　IsingEstimateEnergy_Builtin
　　　　　イジングエネルギーを推定(IsingEstimateEnergy_Builtin)
　

　　　-12.イジングトロッタ(IsingTrotterSample)
　　　　　Implements time-evolution by the Ising Hamiltonian on a line of qubits
　　　　　Q#のFunction　Ising1DExcitationCorrelation
　　　　　エラーで動作せず、サンプルソフトに不具合があるものと思われる。
　　　　　対応方法、IsingTrotterSampleのターゲットCPUをAnyCPUよりX64へ変更
　　　　　Qubit=7,シュミレーション0.1間隔で最大1,Order of Trotter=2

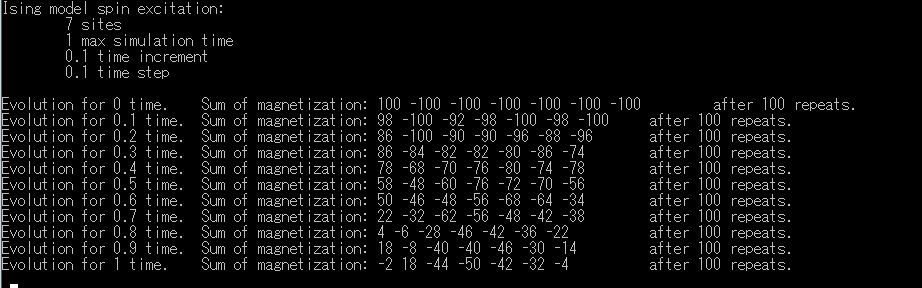
　　　-13.磁化(SimpleIsingSample)
　　　　　Q#のFunction　Ising
　　　　　イジング(Ising)

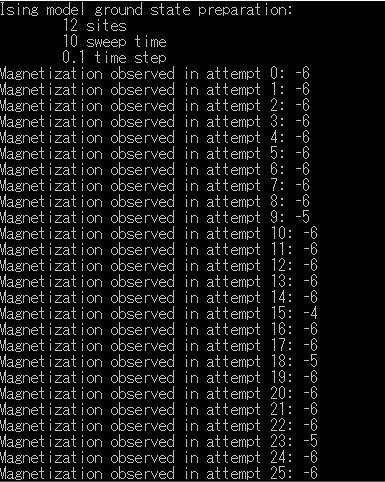
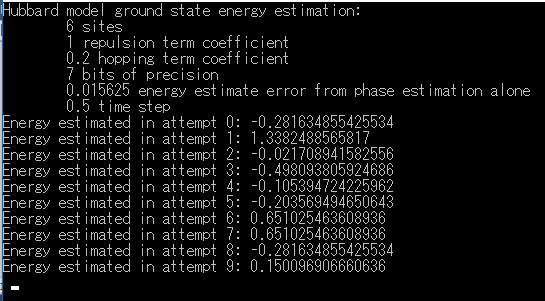
　　　-14.ハバードモデルの量子シミュレーション (HubbardSimulationSample)
　　　　　Q#のFunction　HubbardAntiFerromagneticEnergyEsimate
　　　　　ハバードモデル　　電子相関の効果の強い固体中の電子の振る舞いを量子論的に記述するモデル。
　　　　　(HubbardAntiFerromagneticEnergyEsimate)